Eyes

A tutorial for Python and Pygame Zero 1.2

The eyes follow the cursor.

Drawing an eye

The eye is drawn with a white circle and a smaller dark blue circle for the pupil.

def draw():
    screen.fill((0, 0, 0))

    screen.draw.filled_circle((200, 200), 50, color=(255, 255, 255))
    screen.draw.filled_circle((200, 200), 15, color=(0, 0, 100))

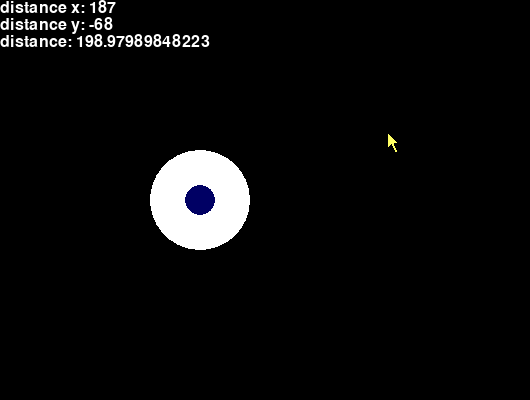
Getting X and Y distance between cursor and eye

The distance between the center of the eye and the mouse cursor is displayed.

The X and Y positions of the eye are reused from drawing the eye, so variables are made for them.

The pygame module is imported so that pygame.mouse.get_pos can be used.

An empty update function is created so that the draw function will update on every frame.

Full code at this point

import pygame

def update():
    pass

def draw():
    screen.fill((0, 0, 0))

    mouse_x, mouse_y = pygame.mouse.get_pos()

    eye_x = 200
    eye_y = 200

    distance_x = mouse_x - eye_x
    distance_y = mouse_y - eye_y

    screen.draw.filled_circle((eye_x, eye_y), 50, color=(255, 255, 255))
    screen.draw.filled_circle((200, 200), 15, color=(0, 0, 100))

    screen.draw.text(
        'distance x: ' + str(distance_x)
        + '\n' + 'distance y: ' + str(distance_y),
        (0, 0)
    )

Getting straight-line distance between cursor and eye

The distance in a straight line is calculated using the Pythagorean theorem.

The square root of the distance on the X axis squared plus the distance on the Y axis squared is the distance in a straight line.

The math module is imported so that math.sqrt can be used.

Full code at this point

import math

def draw():
    # etc.

    distance = math.sqrt(distance_x**2 + distance_y**2)

    # etc.

    screen.draw.text(
        # etc.
        + '\n' + 'distance: ' + str(distance),
        (0, 0)
    )

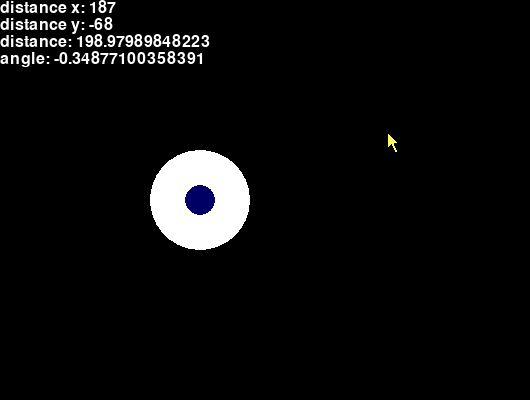
Getting angle between cursor and eye

The angle in radians between the mouse cursor and the center of the eye is calculated using math.atan2.

Full code at this point

def draw():
    # etc.

    angle = math.atan2(distance_y, distance_x)

    # etc.

    screen.draw.text(
        # etc.
        + '\n' + 'angle: ' + str(angle),
        (0, 0)
    )

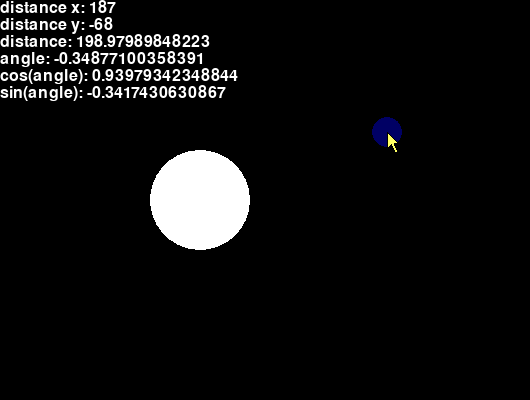
Moving pupil

The cosine/sine of the X/Y positions give the ratio between the X/Y positions and the straight-line distance.

For example, when the mouse is directly below the eye, all of the straight-line distance goes into the Y axis, so the cosine is 0 and the sine is 1.

For another example, when the sine is 0.5, the Y distance is 0.5 (i.e. half) of the straight-line distance, and the X distance is around 0.86 of the straight-line distance.

The pupil is moved by the cosine/sine of the angle multiplied by the distance, which brings the pupil to the mouse position.

Full code at this point

def draw():
    # etc.

    pupil_x = eye_x + (math.cos(angle) * distance)
    pupil_y = eye_y + (math.sin(angle) * distance)

    screen.draw.filled_circle((eye_x, eye_y), 50, color=(255, 255, 255))
    screen.draw.filled_circle((pupil_x, pupil_y), 15, color=(0, 0, 100))

    # etc.

    screen.draw.text(
        # etc.
        + '\n' + 'cos(angle): ' + str(math.cos(angle))
        + '\n' + 'sin(angle): ' + str(math.sin(angle)),
        (0, 0)
    )

Moving pupil maximum distance

The straight-line distance is limited to a certain number so that it can't move outside of the eye.

Full code at this point

def draw():
    # etc.

    distance = min(math.sqrt(distance_x**2 + distance_y**2), 30)

    # etc.

Multiple eyes

The code is made into a function which takes an eye's X and Y positions.

Full code at this point

import pygame
import math

def update():
    pass

def draw():
    screen.fill((0, 0, 0))

    def draw_eye(eye_x, eye_y):
        mouse_x, mouse_y = pygame.mouse.get_pos()

        distance_x = mouse_x - eye_x
        distance_y = mouse_y - eye_y

        distance = min(math.sqrt(distance_x**2 + distance_y**2), 30)
        angle = math.atan2(distance_y, distance_x)

        pupil_x = eye_x + (math.cos(angle) * distance)
        pupil_y = eye_y + (math.sin(angle) * distance)

        screen.draw.filled_circle((eye_x, eye_y), 50, color=(255, 255, 255))
        screen.draw.filled_circle((pupil_x, pupil_y), 15, color=(0, 0, 100))

    draw_eye(200, 200)
    draw_eye(330, 200)